A Proof - With Updates...

That a multi-digit number in Base 10 ending in "1" is less likely to be prime (plus some hexagon considerations)

UPDATE: Edit - tis December 6, 2023 - tis 1047 as I type this - here is a snippet you might appreciate - I know I do.

I think if I ever changed my long-time “icon”, my “moniker” I’ve used to present - “who I am” - Buffalo_Ken - for so many years now and I’ve shown the origin image of it - anyhow, if I ever changed it - I would change it to that image above - what you think it is?

So - since I’ve typed this I might as well provide a link to the place mentioned - it has the original image on it of who I am.

http://www.carbon-tax.us/

You've got to read down to get to the image

~~~~~~~

UPDATE: Edit - tis December 3, 2023 - 12323 and tis 1314 in minute time - so if you want to know what a “tight” space is of pieces connected, then take the 23 shapes with 5 “perfect” hexagons below. That gives what? One hundred fifteen (115) shapes in total (23 * 5) and if a hexagon individual is characterized as “perfect”, then please be aware it is imaginary in a way cause nothing - not even nothing - is perfect. Regardless, going with that premise, each hexagon has a fixed area 2-dimensionally and so the total area when wrapping around the perimeter of any collective shape with all twenty three (23) five-tile-hexagon shapes connected has a lower bound = 23 * 5 * area of a perfect hexagon individual. If you combine the shapes in said manner with no space betwixt, then that would be a top score in the “game” I’m imagining now….so…I thought I’d share that idea. Feedback is desired.

~~~~

UPDATE: Edit - tis December 2, 2023 - 12223 (or 12’223 for “purist”) as I like to state it….and here are all 23 shapes - please tell me if you see one that is NOT discrete.

Shape that was there has been temporarily deleted - proof checking in progress

tis 122323 1919

I’m sure there is a way “easier” to present this and as I’m working on shapes with six (6) tiles each I’ll try to figure that out for the sake of good communication. With that said, no matter how one flips or twists the above shapes - each one is discrete and distinct 2-dimensionally as far as I know assuming I didn’t make a mistake. There is some math buried in this I know.

Now with that just posted above you tell me this - if you took each shape and rotated it around how “tight” could you get the pieces to fit together?

I suspect the “white space” inbetween could be reduced by about 90% if not completely - that is a puzzle in and of itself - are you up for the challenge?

BK, 12223 1641

Consider this - if each shape was a “card” in the deck and they were picked randomly could the players place the pieces to fit together tightly? And if they did and there were no blank spaces in-betwixt, then that means a high score in the game per one way of scoring things…

Can you imagine this - it could be both solitaire or group play!

There are so many options for how this could be a way to learn about shapes natural.

I think I might try to do this for myself and when I do I’ll come back here and present the image tight…..if I do…but looking at the shapes just now and imagining the possibilities - I’m pretty sure they can be connected without any space in be-twixt….but there is some luck to it depending on the “rules” of the game - my initial thought is - pick the pieces one a time randomly and connect them in a manner facilitating a “tight” space - and another question mathematical is - could it be no matter the order the shapes picked that with “proper placement” there will be no space in-betwixt?

I have no idea what the answer is!

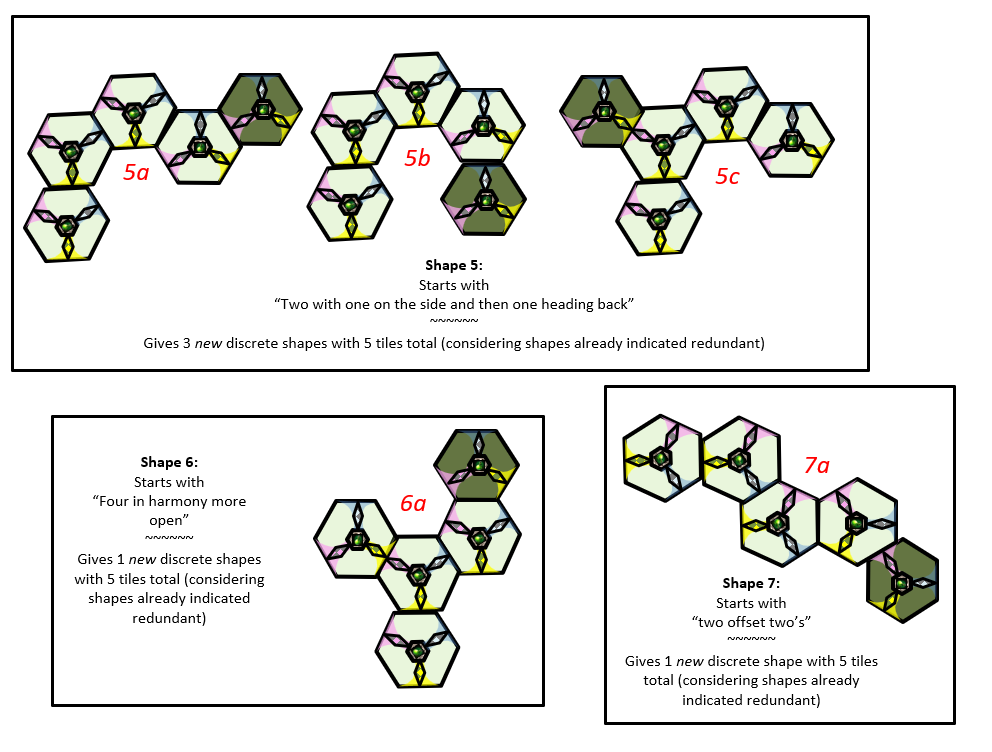
Sometimes you might as well finish what you start - here are the final shapes I think when 5 hexagons are connected 2-dimensionally - there are five “new” shapes in these images as I’ve gone back in forth making corrections and if I got my shapes correct finally - that gives a total of 23.

Please point out any mistakes if you see them, but I’m pretty sure 23 is the number of shapes with 5 hexagons independent of orientation and now that this is down here and published - I reckon tis time to move on to the possibilities when six hexagon tiles are connected….

(a little edit here - 122523 1514 - I’ll never tell unless you ask!)

Tis presently 112523 and tis 7:48 pm and I’m done for today…

~~~~~~~~~~

OK, I decided to try, I’ll come back and check for mistakes later, but here is the next two shapes on the way to 23 total:

This can be trick avoiding redundancy, but I’ll come back and double-check…

Last edit for today - tis 1843 - this is ridiculous, I’m correcting what I got correct in the first place - must mean tis time to take a little rest on this…

I’m fond of “Shape 4” - it ain’t its fault it came later in diagnosis, but sure enough it is redundant with shape 2c below.

other corrections have been made I believe - but I’ll double check again…

(122323 1928)

~~~~~~~

OK, so after making it through 4 of the shapes made with 4 tiles, the number of shapes discrete with 5 tiles is:

4 + 10 + 4 + 0 when adding it up with those four starting shapes accordingly. So that gives 18 shapes so far - there are five more to be discovered assuming I haven’t made any errors, but I’ll come back here and double-check my work and get the numbers accurate and provable. That 4th shape - I wasn’t sure for awhile and I’m still not totally sure, but it helps to practice and this methodology is easily proven - in the real world - the macro world - the world we all can sense. That in contrast to “quantum physics land of imagination” has beauty easily understood in my mind.

OK - c u later…

112523 1851

~~~~~~~~

Here is the next set of hexagon shapes connected five tiles.

(Edit - 122323 1917 - I just found an error in the image that was below - here is a “correct” version - but now I got some other things to “double-check”)

I know I might have some typos or there could be mistakes, but after I get through doing all of this, I’m gonna post an article with the proof up to six hexagons - and it will be double-checked no doubt and accurate and my guess is the total number will be prime.

~

Here is the latest update: 112523 1329

Here is the proof (see below):

(Edit tis November 24, 2023 or 112423 per nomenclature I prefer - more detail on the hexagon question discussed below is presented in this image that shows the 7 possible discrete 2-dimensional images that can be made with hexagons independent of orientation - it is a fixed number and anybody can figure this out on their own - that in a way is the beauty of it I think…)

Do you see - there are four (4) hexagons connected in each combined shape and there are a total of seven (7) discrete shapes total 2-dimensionally. You can ignore the images within the shapes, but they make for a good game potentially - the main question I have is how many discrete shapes are there when there are eight (8) hexagons in total connected 2-dimensionally. When there are five (5) hexagons, the number of shapes is 23. I’ll solve it for six (6) hexagons soon enough.

Meanwhile, I’m becoming an advocate for propane as a good fuel for those who choose to be self-sufficient.

It was posted per the following time stamp:

2023 - 11 - 12T20:10:50Z

This was about 9 days ago….so must of been

111223 1450 per my “nomenclature” - November 12 was “9 days ago” was it not? I just snipped the image above - so you figure it out. It came from here:

https://www.sott.net/article/157471-Stonehenge-builders-had-geometry-skills-to-rival-Pythagoras

~~~~

You know there are some of us love our children more than you could ever imagine assuming you don’t love your children like we do.

~~

Below is the 2nd heater I got setup today:

Propane heat - easy to setup for the everyday man. It fits in here at our getaway place in the forested hills by the river.

~~~~~~~~~~ Edit - 112523 1039 ~~~~~~~~~~

OK, it is November 25, 2023 10:39 am (give or take) Eastern US time, and I am having fun presenting some harmless mathematical ideas I’ve been “stewing” over for quite some time - especially with respect to the “hexagon puzzle” (see Comments below for additional detail). So, with my recognition yesterday that I could simply present images using tools I already have hand, below is the first image showing how the number of discrete shapes (independent of orientation) with five “perfect hexagons” connected can be determined. It starts with one of the shapes presented above when there were four connected hexagons and then presents the possible “new” shapes that can be made when adding a 5th tile. So if you recall, there were a total of 7 shapes with 4 tiles connected (per the image at the top of the article), and I will work through each of them and show the “new” shapes when there a 5th tile is connected (green fill). It is important to remember previous shapes already created so that only discrete shapes get counted.

More to follow…..although I may just go ahead and dedicate a post to this hexagon puzzle so as not to get too mixed up with the prime number considerations….

This now 10:50 am.

~~~~~ Edit - English Heritage Scarf for Sale - ~~~~~~~~

Get it here: https://www.english-heritageshop.org.uk/mosaic-scarf-viscose-65-x-180cm

~ an edit with attitude aplenty ~

Stonehenge is a place of geometry no doubt. The time now with this “edit” as I said I would, cause I ain’t kidding around is 81124 - eight one one two four.

BK